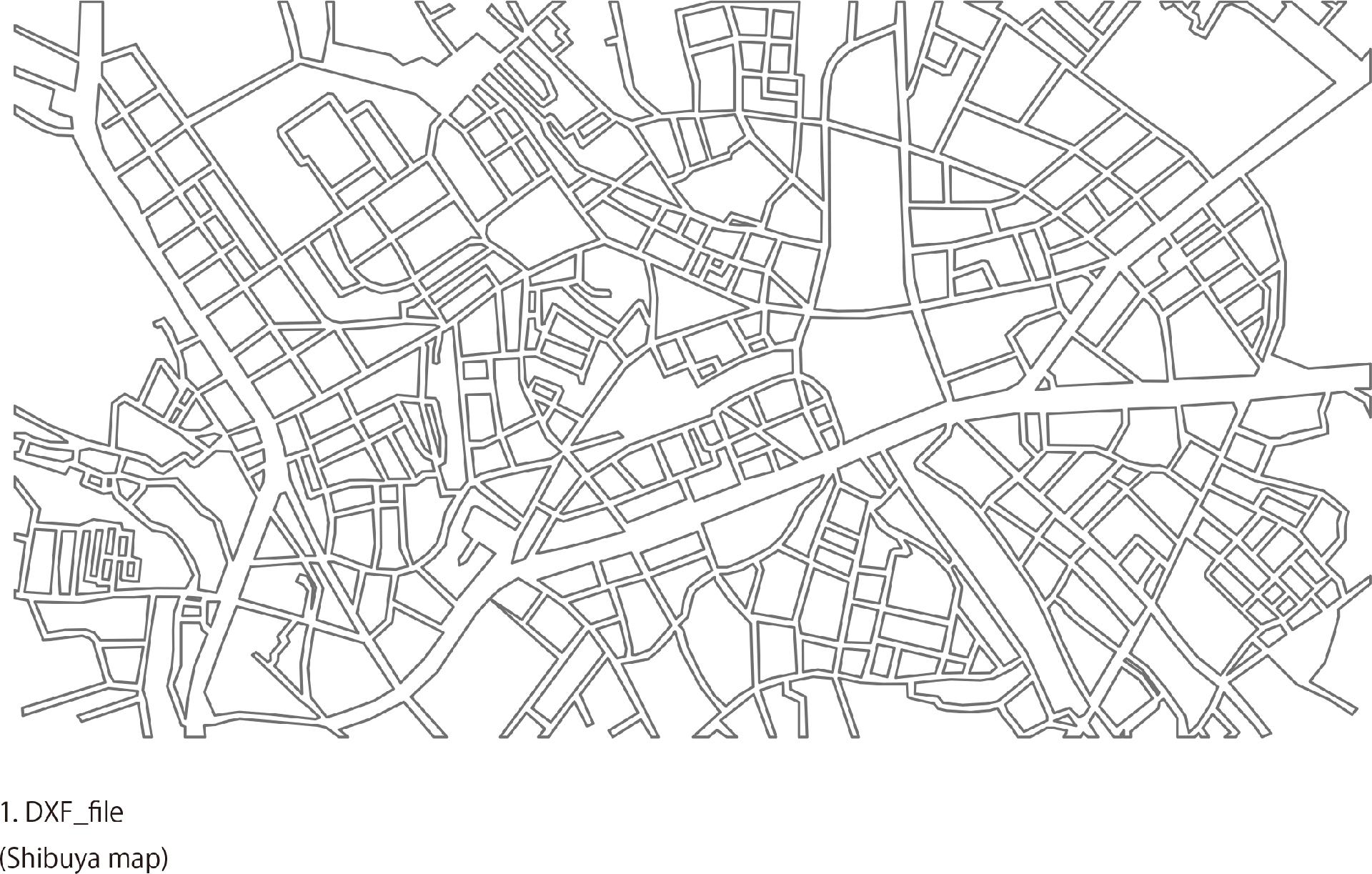
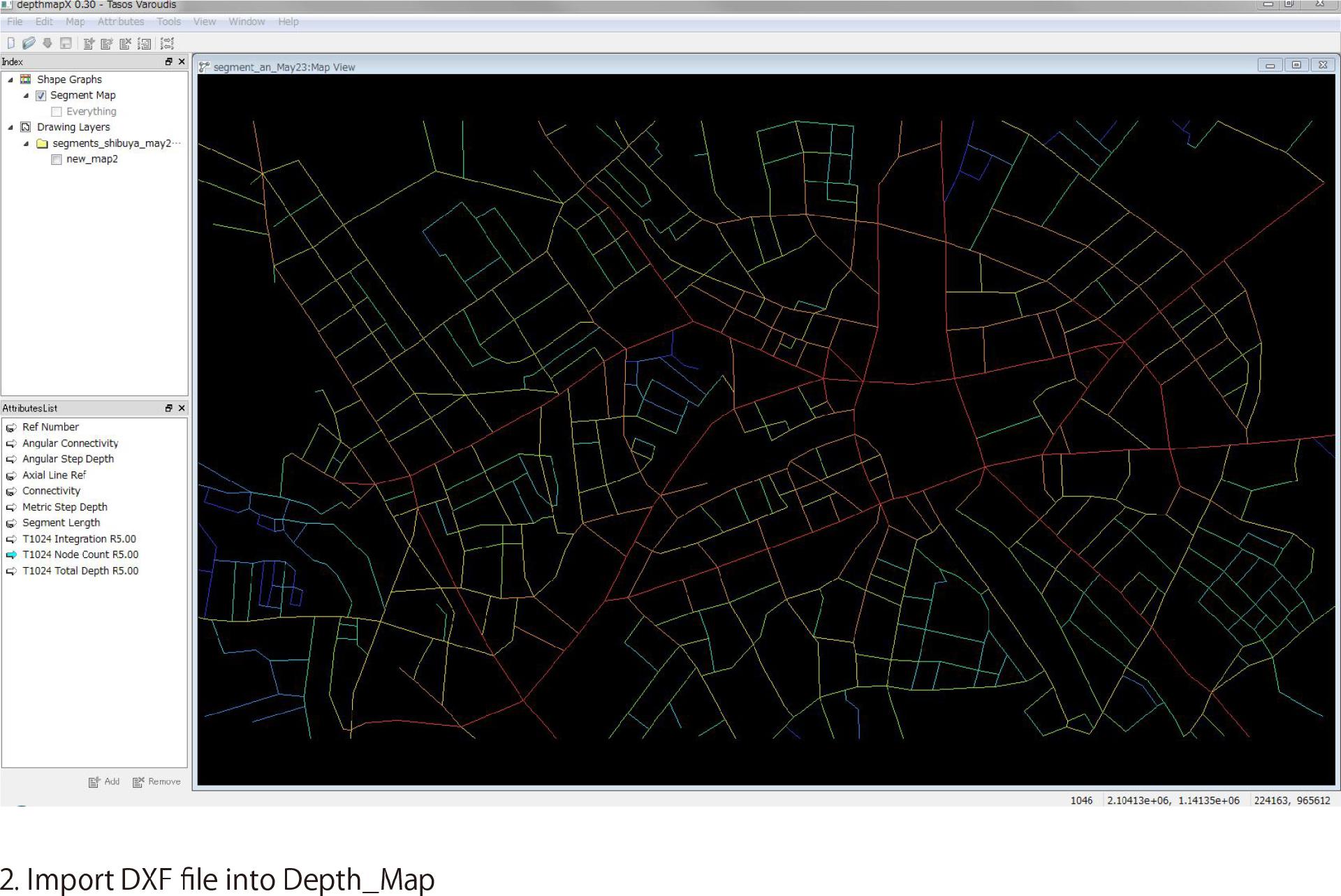
In this post we gonna describe what is Depthmap and how to use it in order to run analysis of the space. Depthmap is a software for spatial analysis. It works at different scales of the space such as: building, city or whole region. In this case the choosen space for analysis is part of Tokyo city - Shibuya area. As an input it takes a 2D plan (building plan or city plan), which must be saved as DXF file. Then drawing should be converted into segment map In order to run the analisys. After file imported into the Depthmap environment it should be saved as graph file.
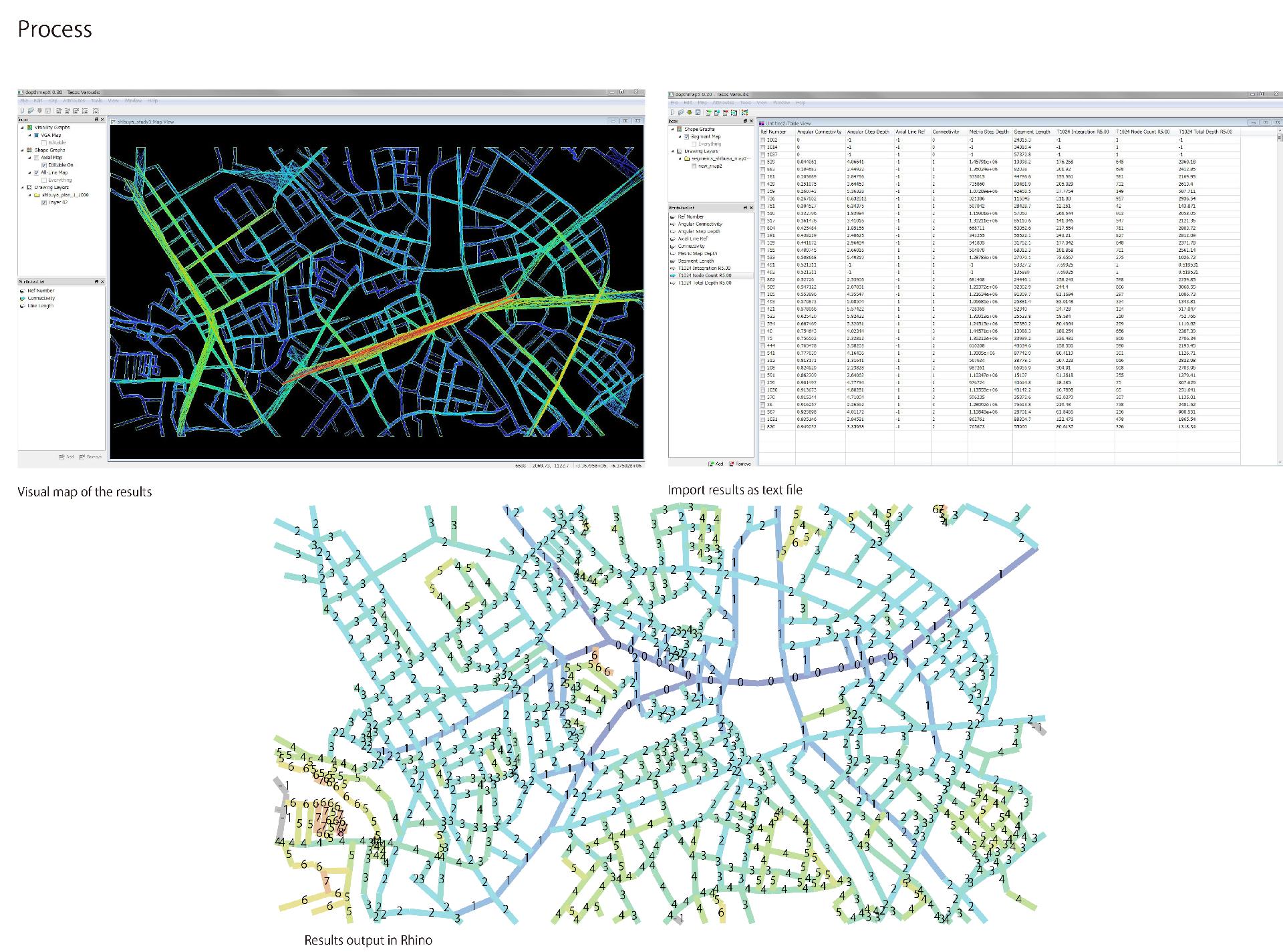
The general idea is that all the spaces divided into segments(or components of the space) and then analysed as a network. When analysis is finished all the results represented as visual maps showing different aspects such as: integration of the segments in relation to each other, connectivity, angular connectivity, angular step depth, metric connectivity, step depth. And all the data can be exported as txt file with all the analysis values and used for father studies.
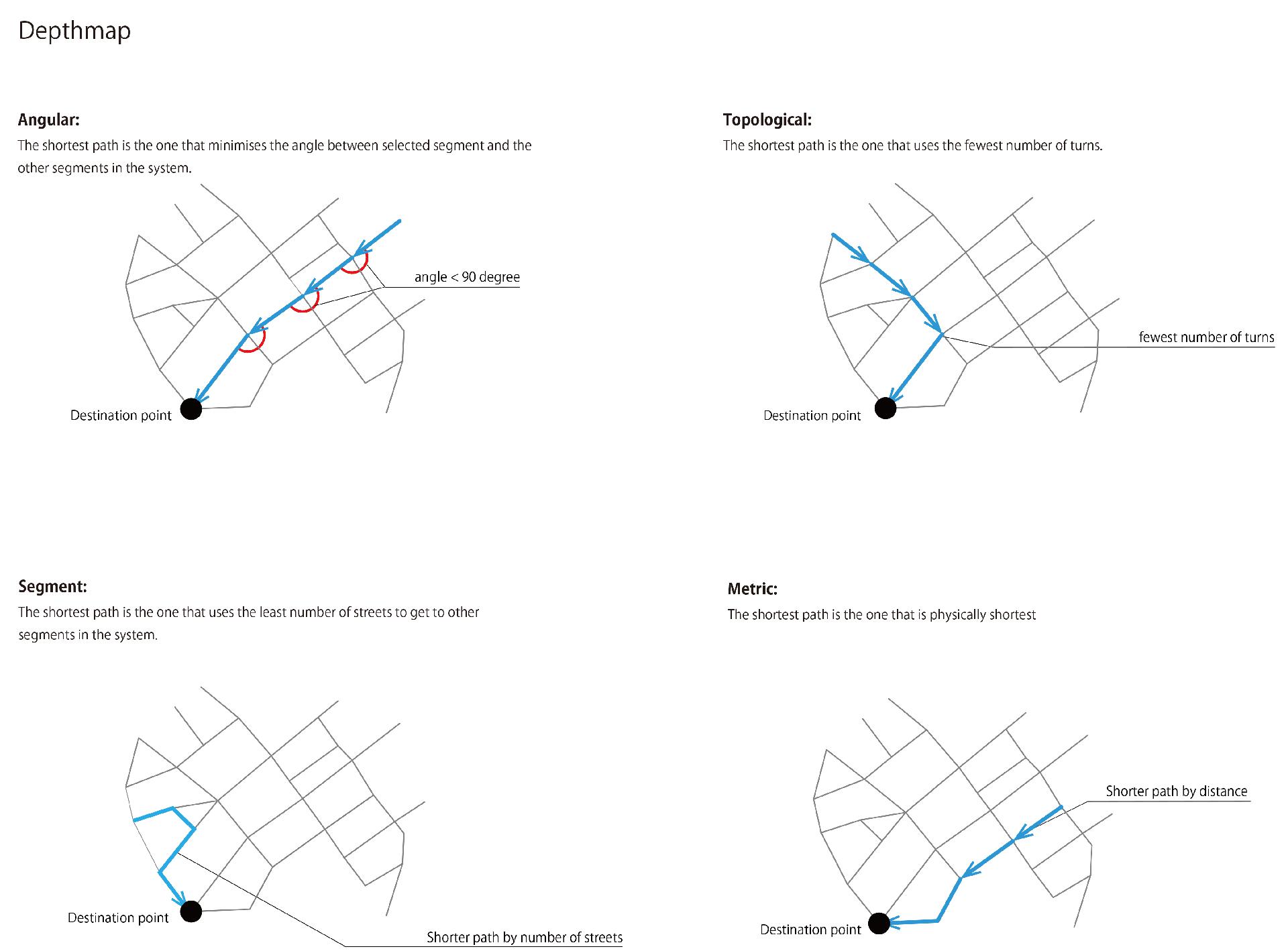
Analysis in Depthmap finds the shortest path between one node(in this case a street) and series of other nodes(streets) in the system.
Shortest path can be defined in a number of ways:
Angular:
The shortest path is the one that minimises the angle between selected segment and the other segments in the system.
Topological:
The shortest path is the one that uses the fewest number of turns.
Segment:
The shortest path is the one that uses the least number of streets to get to other segments in the system.
Metric:
The shortest path is the one that is physically shortest.
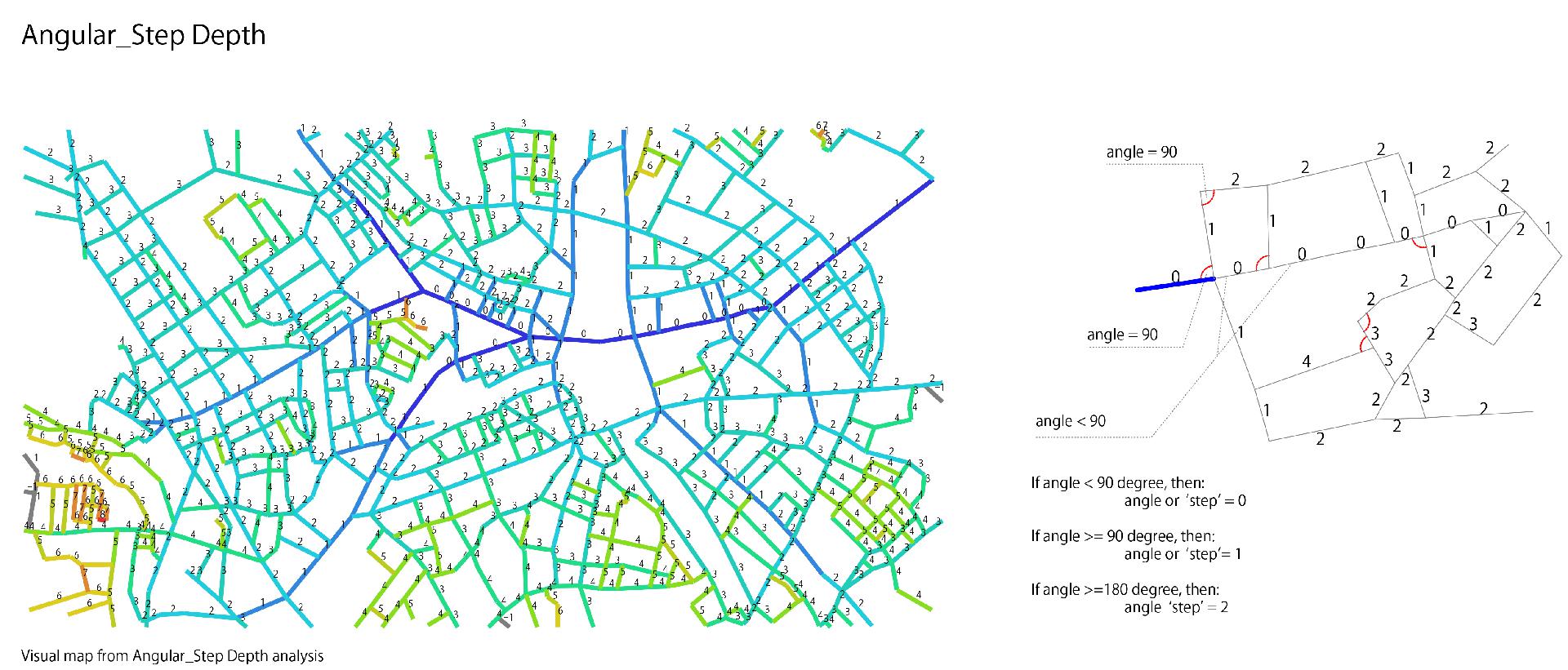
Angular step depth
follows the shortest angular path from the selected segment to all other segments withing the system. If the segment carriers straight on to another segment then the angular turn costs 0 steps. If the segment turns 90 degree to get to another segment, the angular turn costs 1 step. And if the segment has to double back in the opposite direction (turn of 180), the angular turn cost 2 steps. Angular scale used, '1 step' is 90 degree, and angles are cummulative. If to turn left 45 degree and walk for a segment lenght and then turn right 45 degree in total is 90 degree, exactly the same as if to turn on 90 degree left or right.
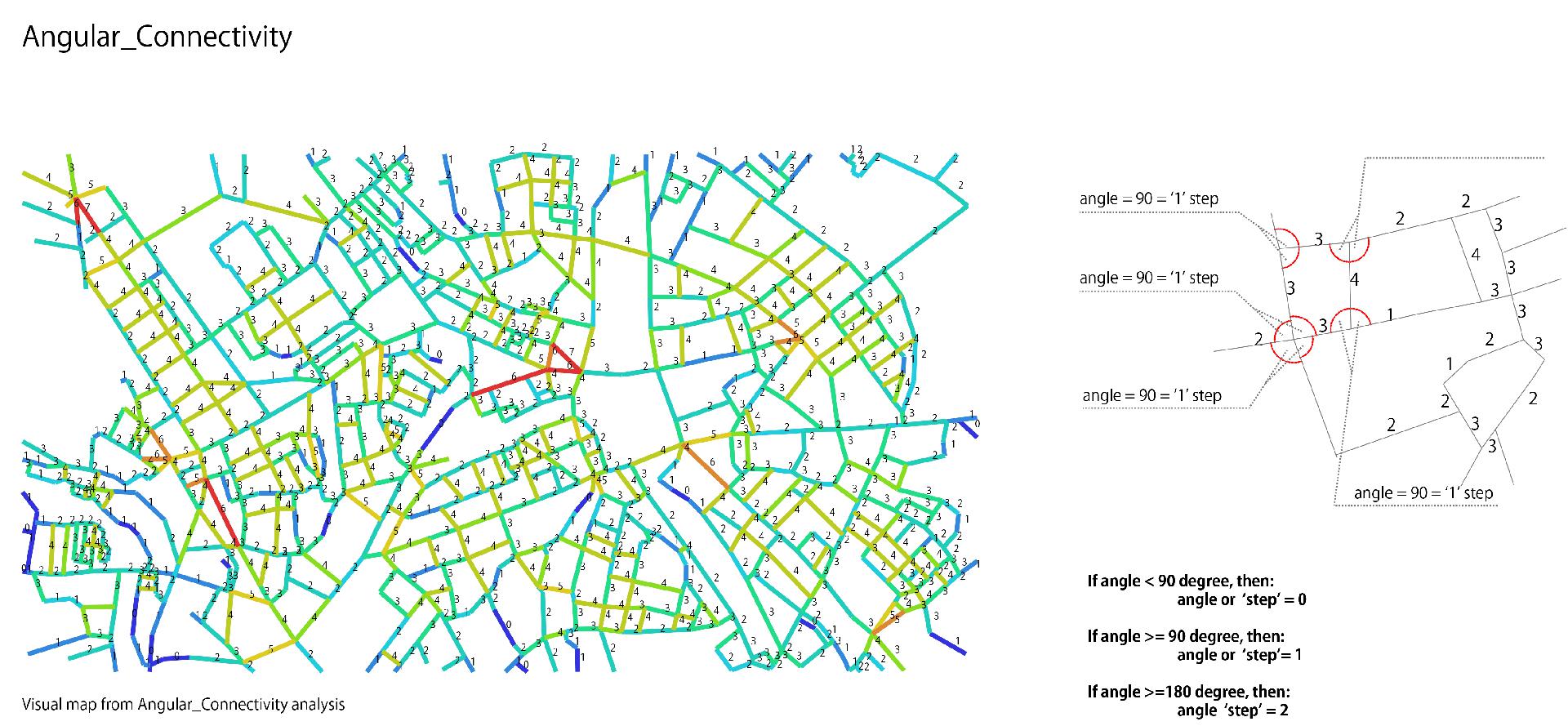
Angular connectivity
It is the cummulative turn angle to all other lines
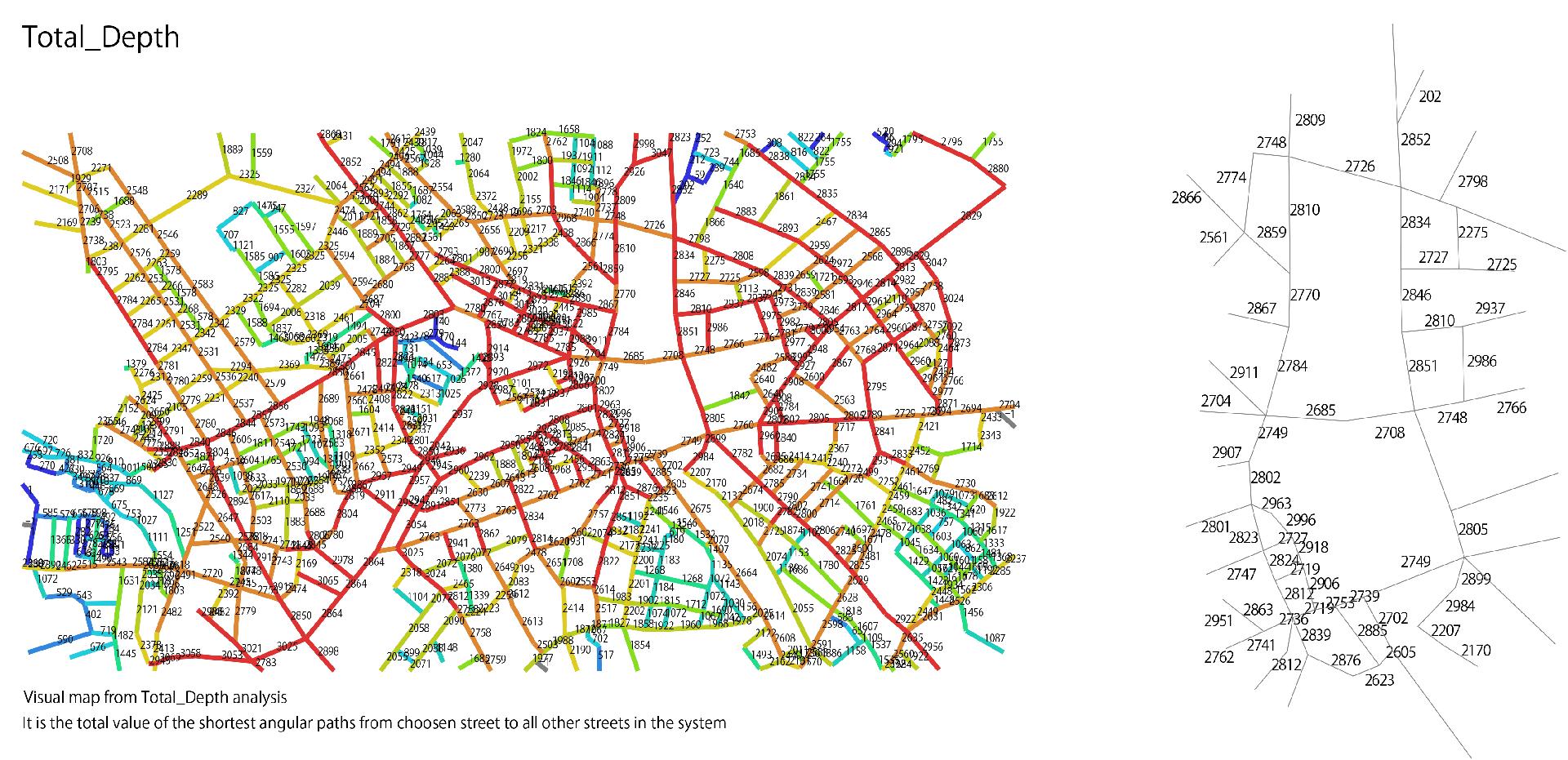
Total angular depth
It is the total value of the shortest angular paths from choosen street to all other streets in the system.
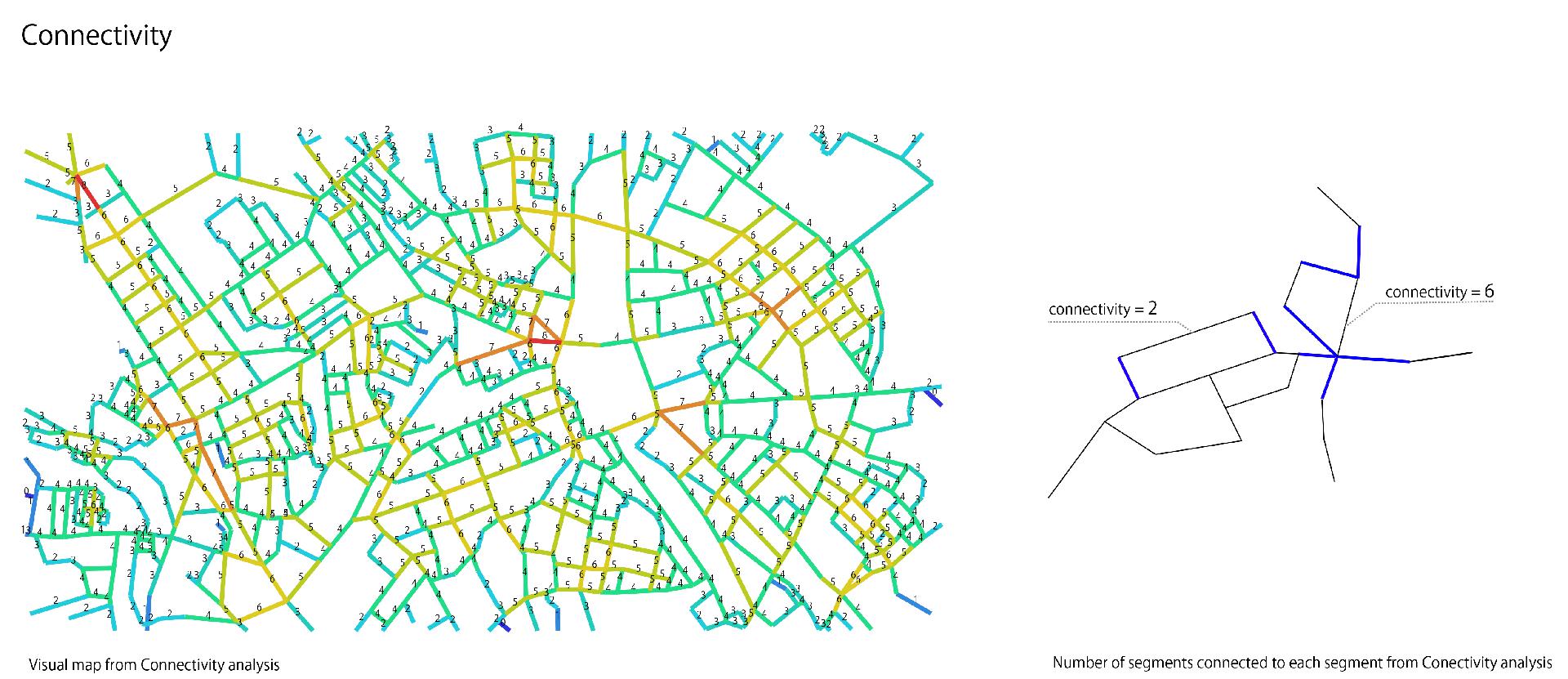
Connectivity
Is a number of segments connected to each segment in the system.
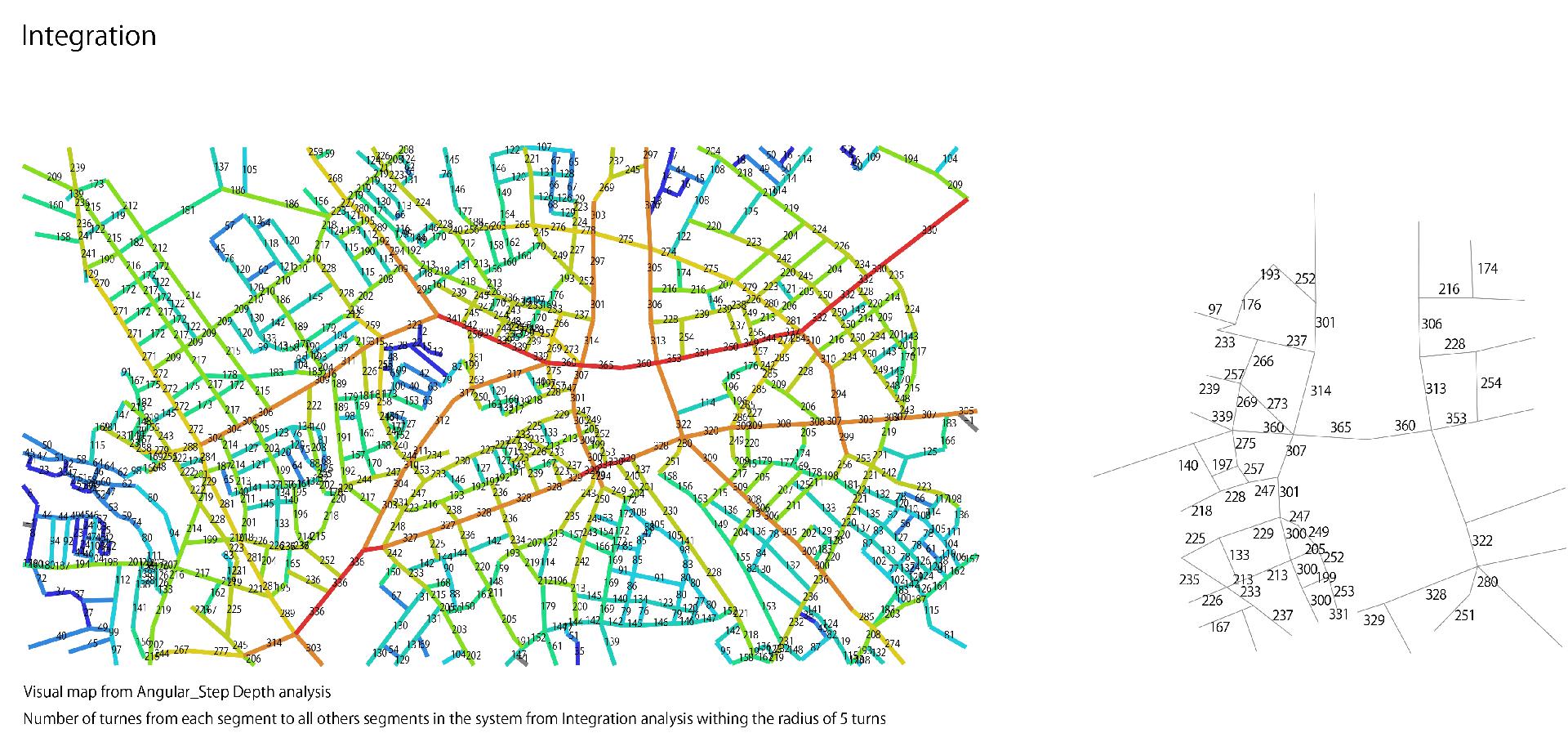
Integration
Measures number of turns have to be made from a street segment to reach all other street segments in the network, using shortest paths. The street segments that require the fewest turns to reach all other streets are called 'most integrated' and are usually represented with hotter colors.
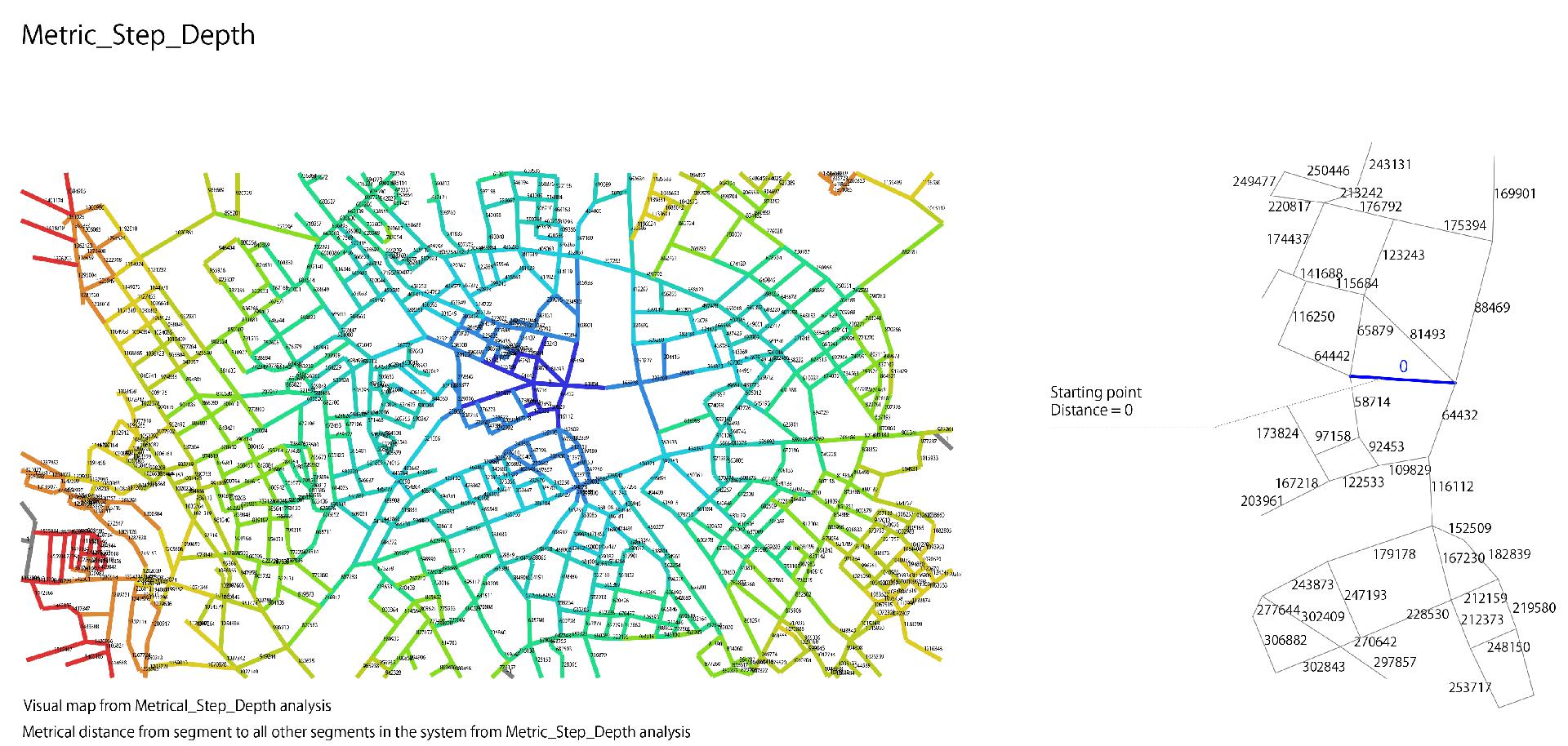
Metric step depth
The result shows the distance value between choosen street to all other streets in the system.


コメントをするにはログインしてください。