はじめに

こんにちは．忘年会の季節ですね．私のいる階では12月3日に忘年会が開催されるので，1年の92.3%を忘れられる計算です．

冗談はこれくらいにして，パーティーの場所決めは難しい問題です．ざっと思いつくのは，次のような条件でしょうか．

• アクセスがよい


• 料理のクオリティが高い


• 値段が安い

このうち，2番目と3番目はとりあえず置いておくとして，1番目について考えます．全員が集まるためには，なるべく全員の家や職場からの距離が近いほうが会場として望ましいですね．つまり，この問題は以下のように書くことができます．

「参加者全員の家から，会場までの移動コストの和を最小化する点を求める」

移動コストとして，たとえば次のようなものを考えることができます．

• 直線距離


• 道沿い・線路沿い距離


• 運賃

このリストは，上から下に向かって問題が難しくなっていきます．
まず，直線距離を求めることは比較的簡単にできます．次に，道沿い・線路沿いの距離を求めるためには，道路や鉄道のデータをグラフ形式で与える必要があります．最後に運賃ですが，これはさらに難しい問題です．上2つと違って，運賃はしばしば階段状に変化します（不連続）し，遠回りルートのほうが安い（距離の公理を満たさない）など，さまざまな問題があり，とても扱いが厄介です．たいへんですね！

そんなわけで，今回は直線距離を題材に問題を考えてみます．この場合，問題は以下のようになります．

「参加者全員の家から，会場までの直線距離の和を最小化する点を求める」

実際に解いてみる

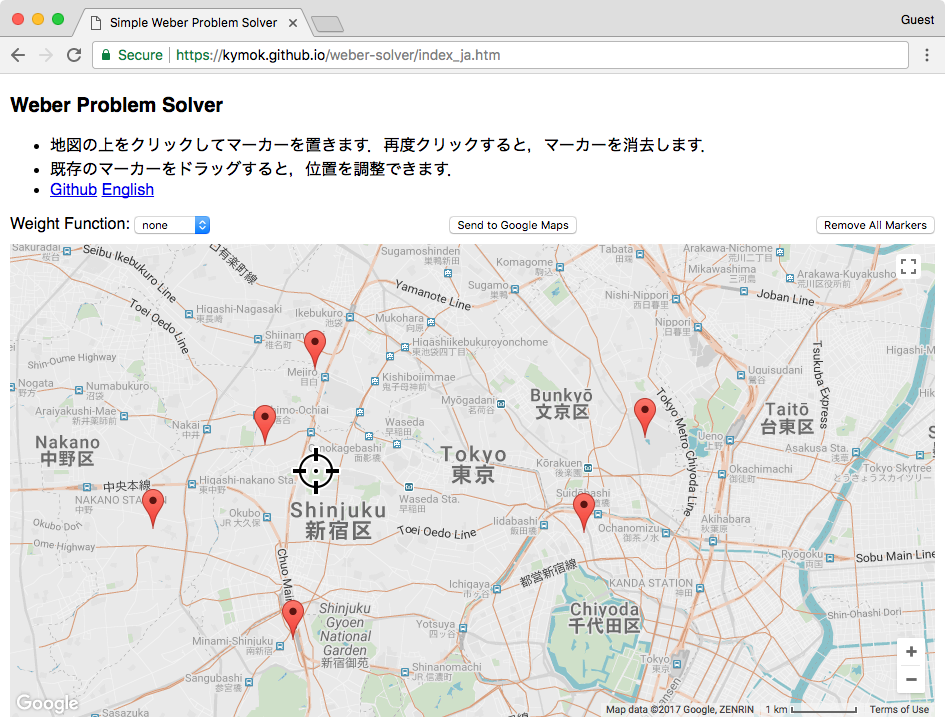
では，実際に計算機を使って解いてみましょう．まず，ブラウザでデモページを開いて，地図上を何点かクリックしてみてください．十字カーソルが出てきた点が問題の答えです．

ソースコードは Github 上のページをご覧ください．ここでは，簡単に解き方の概要を説明します．

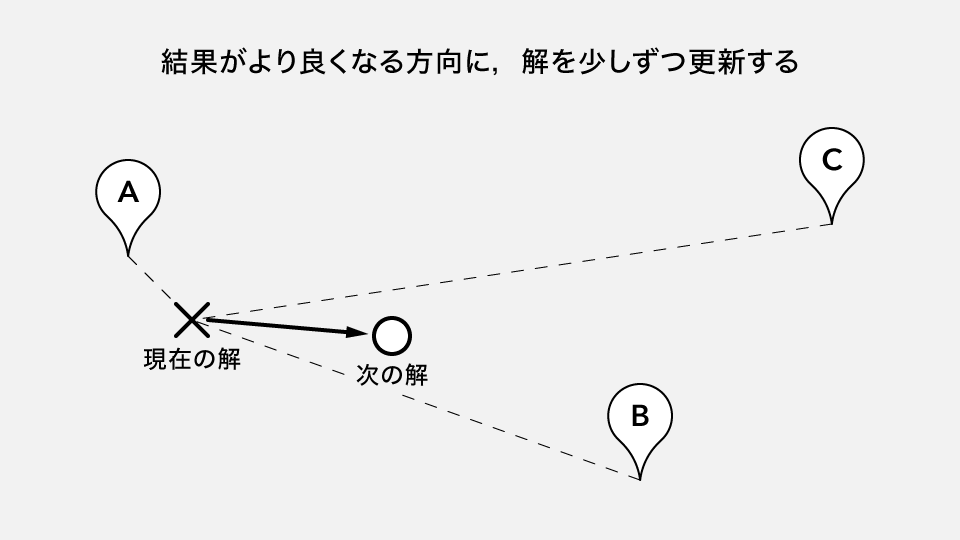
1. まずは，適当なところに仮の解をおきます（図のX印）．


2. この解をどの方向に移動したら，最も解が改善するかを計算します（図の矢印）．図の例では，右方向に移動すると，点Aからの距離が長くなるかわりに，点B，点Cからの距離が短くなるので，全体としては距離が短くなりそうです．


3. 解を移動して，最初に戻って計算します．

このように，繰り返し計算をして解を求める方法を，逐次解法と呼びます．この計算は基本的には終わりがないので，改善の幅が小さくなったり，行ったり来たりを繰り返すようになったりしたら計算を打ち切って，結果を最終的な解として返します．

おわりに

このソルバーを忘年会の位置決めに応用することには，いくつかの欠点があります．
たとえば，公平性をまったく考慮していないので，解の配置は露骨に多数派に寄ったものとなります（試してみてください）．この例に限らず最適化手法では，目的関数をうまく設定しないと，良くも悪くも予想もしなかった解が求まることがあります．そこから問題の性質を読み解き，譲れない条件，変えてもよいもの，等々を考えながら結果を解釈し，最終的な判断を下すことになります．

参考書籍

• 岡部篤行, 鈴木敦夫 (1992). 最適配置の数理. 朝倉書店.